Приложения

Приложения

ПРИЛОЖЕНИЕ А: Радиальные и направленные числа

Богатство радиально-обратных отношений тринадцати чисел еще более расширяется, если рассматривать числа ряда 1-13 (или 13-1) не просто последовательными, но и связанными с определенными направлениями. Пусть первому числу 1 соответствует Восток (В), числу 2 - Север (С), числу 3 - Запад (3), числу 4 - Юг (Ю), пятому - вновь Восток, и так далее. Тогда ряд 1 -13 можно записать с указанием направлений:

Достигая числа 13, пульсация возвращается к 1, но указатели направлений продолжают сменяться в своем цикле:

Для того чтобы 1 вновь совпало с В, необходимы 52 перестановки (произведение 13 чисел и 4 указателей направлений). Кроме того, можно считать, что собственный цикл указателей направлений состоит из 5 круговых оборотов, то есть для завершения такого цикла последовательность В-С-3-Ю должна повториться 5 раз, что составляет 20 позиций - здесь число 20 является не только произведением 4?5, но и суммой чисел 7 и 13, двух ключевых «мистических» чисел, входящих в ряд 1-13.

В этом случае возникает матрица Цолькин, состоящая из всех 260 возможных перестановок, образуемых круговым вращением 13 чисел, проходящим через 20 позиций указателей направлений. Если каждое из тринадцати чисел связать с отдельным качеством тона, изменяющимся в соответствии с 20 позициями, то перестановки превращаются в описание всего богатства гармоник, а 260 элементная матрица становится многофазной клавиатурой, позволяющей исполнить галактическую симфонию!

ПРИЛОЖЕНИЕ Б: Множители и фракталы в Системе Майя

Простыми словами, фрактал представляет собой постоянно сохраняющуюся пропорциональность. Например, 36-градусный сегмент круга всегда остается равным 36 градусам, независимо от изменений диаметра окружности. Кроме того, такой сегмент содержит информацию, достаточную, чтобы восстановить по нему всю окружность. Фрактальный принцип означает голографическую природу бытия: по доступной части чего-то целого можно воссоздать все целое.

Этот принцип справедлив и для обертонов. Точно так же, как тон одной октавы способен отражаться, находить отклик в других октавах, несмотря на то, что тоны различных октав звучат с разными частотами, так и делитель числа, или одно число из последовательности может «звучать» на многих уровнях, порождая сходные, пропорциональные обертоны. Интересно, что при звучании 16-тоновой гаммы, на нее откликается лишь единственный тон всей матрицы обертонов - тринадцатый.

Приведем примеры. 13 является фракталом 130 (= 13?10), 144 - фрактал 1440 (= 144?10). Это означает, что с помощью числа 13 можно воссоздать 130, и наоборот, из 1.440 можно извлечь 144. Фракталы 13 и 144 образуют серию пропорций, которые остаются постоянными для всего бесконечного ряда кратных им чисел.

Таким образом, любое число образует бесконечный фрактальный тональный ряд, к примеру, 26, 260, 2600, 26000 или 52, 520, 5200, 52000. Важно то, что фрактальный ряд определяется не количественными характеристиками числа, но качеством основного фрактала, определяющего ряд - 13, 26, 52 и так далее - и создающего пропорциональный «тон» всего ряда. Количество нулей в числах фрактального ряда можно рассматривать как мерило высоты этих тонов, увеличения их частот.

С фракталами связаны множители - числа, на произведение которых раскладывается другое число. Например, 260 представляет собой результат произведения делителей 13 и 20. В то же время, 260 является членом фрактального ряда, основанного на 26, которое, в свою очередь, можно представить в виде 13?2. Все фракталы являются общими множителями чисел своего фрактального ряда и, одновременно, способны образовывать множество фрактальных рядов с различной сохраняемой пропорцией.

Внимательное рассмотрение позволяет выявлять взаимопроникновение различных чисел. Например, число 144 можно разложить на множители следующим образом: 12?12, 9?16, 18?8, 3?36 или 72?2, а число 52 представляется в виде 13?4 или 26?2. Практически, все ключевые фракталы майянской системы связаны с множителями 13, 4 и 9. Так, 260 = 13?20, 64 = 4?16, а 144 = 9?16. В результате, разнообразие делителей больших целых чисел является мерилом степени их гармоничности.

ПРИЛОЖЕНИЕ В: Календарные гармоники

   360 элементный «календарный» период под названием тун проставляет собой третий позиционный разряд майянской числовой последовательности, основанный на множителе 9. Эта последовательность, во всех остальных случаях образуемая множителем 20, бесконечна, но в практических целях используются ее первые девять членов, приведенные ниже с указанием майянских наименований соответствующих разрядных позиций и временной продолжительности[9] :

9. Алавтун [Alautun] = 23 040 000 000 кинов (или 20 кинчильтунов); приблизительно 63 040 000 лет

8. Кинчильтун [Kinchiltun] = 1 152 000 000 кинов (или 20 калабтунов); приблизительно 3 152 000 лет

7. Калабтун [Calabtun] = 57 600 000 кинов (или 20 пиктунов); приблизительно 157 600 лет

6. Пикгун [Pictun] = 2 880 000 кинов (или 20 бактунов); приблизительно 7 900 лет

5. Бактун [Baktun] = 144 000 кинов (или 20 катунов); приблизительно 394 земных года

4. Катун [Katun] = 7 200 кинов (или 20 тунов); приблизительно 19 лет

3. Тун [Тиn] = 360 кинов(или 18 = 9?2 виналей); приблизительно 1 земной год

2. Виналь [Vinal] = 20 кинов (20 дней)

1. Кин [Kin] = 1 кин (1 день)

Если бы эта последовательность увеличивалась без «нарушения» в третьем разряде, тун равнялся бы 400 кинам. Однако при переходе от биналя к туну вводится множитель 9, и тун равен 18, а не 20 виналям, то есть 360 кинам, или дням. Далее последовательность вновь возвращается к стандартному закону увеличения в 20 раз, хотя и несет в себе «искажение», вызванное появлением множителя 9 между вторым и третьим разрядами.

Приведенные девять членов возрастающей последовательности представляют собой систему Майя, откорректированную ими специально для исчисления временных периодов на Земле, а число 9 связано с самой концепцией времени. В любом случае, этот ряд является отклонением от «чистого счета» Майя. Наша позиционная математика десятична, то есть основана на кратных числа 10, а майянский «чистый счет» двадцатиричен, основан на числе 20, и представляется следующими «круглыми» числами, или разрядами:

9 разряд: единица равна 25 600 000 000 (20 ? 1 280 000 000)

8 разряд: единица равна 1 280 000 000 (20 ? 64 000 000)

7 разряд: единица равна 64 000 000 (20 ? 3 200 000)

6 разряд: единица равна 3 200 000 (20 ? 160 000)

5 разряд: единица равна 160 000 (20 ? 8 000)

4 разряд: единица равна 8 000 (20 ? 400)

3 разряд: единица равна 400 (20 ? 20)

2 разряд: единица равна 20 (20 ? 1)

1 разряд: единица равна 1 (1 ? 1)

Отметим, что фрактальные числа «чистого счета» Майя - 2, 4, 8, 16, 32, 64 и так далее - представляют собой последовательность степеней двойки, в которой каждый член является удвоенным предыдущим: 2+2 = 4, 4+4 = 8, 8+8 = 16 и так далее. Эта последовательность лежит в основе перестановочной математики ДНК и Ицзина.

Вернемся к «календарю» и его числам. Как уже отмечалось, 260- и 360-элементный «календари» основаны на ключевых числах 4, 9 и 13. Число 4 символизирует меру, 9 является числом периодичности, или завершенности; число 13 олицетворяет движение, свойственное всему сущему. Разумеется, разностью 13 и 9 является 4.

Число 7, расположенное посередине между 13, является мистическим числом, пронизывающим бытие, а число 5, разность 9 и 4, представляет собой число центра, то есть точку отсчета, от которой отмеривается все сущее, например: четыре направления, четыре времени года и так далее. Такое значение основано на том, что 5 есть сумма 4, числа меры, и 1, числа единства.

Значение каждого числа частично зависит от того, суммой каких чисел оно является. Число 2 (1+1) является числом выраженной полярности, в то время как 3 (2+1) означает принцип ритма. Число 6 (3?2 или 3+3) представляет собой число ритмической целостности, а 8 (4+4), то есть «удвоенная мера», является числом октавы, ключевым числом резонансной гармонии. 10 (9+1) олицетворяет принцип проявленности; 11 - принцип рассогласования;- принцип динамического покоя.

ПРИЛОЖЕНИЕ Г: Гармонические числа

Принцип гармонических чисел, как упоминалось в Приложении Б, заключается в том, что степень гармоничности большого целого числа определяется по спектру фрактальных множителей, на которые это число разлагается. Рассмотрим пример числа 936000, представляющего собой середину Великого Цикла. Дата 6.10.0.0.0, означающая истечение шести с половиной циклов по 144000 кинов, или дней, относится к гармонике 936, поскольку от начала Цикла в 3113 году н.э. прошло 936000 (6.5?144000) кинов. Кроме того, ключевым фракталом числа 936000 является 26:936000 = 2600 тунов по 360 дней в каждом. С точки зрения нумерологии, дата 936000 кинов имеет арифметический корень 9 (9+3+6=18=1+8), как и все числа, кратные 9.

Величайшим гармоническим числом является число 1366560:

1366560/360 = 3796 тунов (тун = 360 кинов).

1366560/365 = 3744 Хааб ([Нааb], земной год = 365 кинов).

Разность между 3796 тунами и 3744 Хаабами равна 52 (13 х 4), а число 52 олицетворяет «календарный круг» с синхронизирован ной продолжительностью в 52 земных года и 73 цикла Священного Календаря, один цикл которого равен 260 дням.

1366560 / 72 = 18980, количество дней в 52 летнем «календарном круге», которое равно 52?365 и 260?73.

1366560 / 73 = 18720 = 52?360 = 260?72

1366560 / 9, число Властелинов Времени = 151840.

151840 кинов / 365 = 416 - неполный земной год, Хааб.

1366560 / 260 = 5256 Цолькинов, или циклов Священного Календаря.

1366560 / 584, число дней года Венеры = 2340 венерианских лет.

1366560 / 780, число дней года Марса = 1752 марсианских года.

1366560 / 2920 дней = 468 циклов совпадения венерианских и земных лет. 2920/365 = 8; 2920/584 = 5.

1366560 / 37960 = 36 циклов по 104 года. Период в 104 года соответствует полному соединению циклов обращения Венеры вокруг Солнца, циклов Священного Календаря и земных лет.

1366560/52 = 26280, или 72 неполных земных года.

1366560 /12 = 113880, или 312 неполных земных лет.

1366560 /13 = 105120, или 288 неполных земных лет.

1366560 / 8 = 170820, или 468 неполных земных лет.

Этих примеров вполне достаточно для того, чтобы оценить поразительные свойства гармоники 136656, совмещающей такое огромное число различных множителей и значений планетарных циклов.

Если отсчитать 1366560 дней от начальной точки, 3113 года до н.э., мы получим дату 9.9.16.0.0, или 631 год н.э. Эта дата соответствует 3796 тунам, по 360 дней в каждом, и 3744 Хаабам, 365 дневным земным годам. Разность между 3796 туновым и 3744-летним циклами составляет 52. Добавив 52 года, полный «календарный круг», к дате 9.9.16.0.0, 631 год н.э., получим дату 9.12.8.13.0, или 683 год н.э. Число дней, истекших с 3113 года до н.э., начала Великого Цикла, по 683 год н.э., равно 1385540, что эквивалентно 3796 неполным земным годам (под «неполным» понимается земной год без учета високосных поправок). Число 1385540 соответствует, кроме того, 73 52 летним циклам «календарного круга». Число 73 представляет собой количество 260 дневных циклов Цолькина, синхронизирующихся с 52 земными годами - это согласование и является «календарным кругом» (52?365 = 260?73). Таким образом, дата 683 года н.э. является фрактальным обертоном «календарного круга». С другой стороны, число 1366560 и соответствующая ему дата 631 года н.э. представляет собой 73 туновый цикл, по 52?360 элементов. Неудивительно, что возникший в 631 году и ушедший в 683 году н.э. Пакаль Вотан неразрывно связан с волшебным числом 1366560!

Наконец, число 1366560 означает завершение 36 венериано-земного цикла протяженностью в 104 года (104?36 = 3744 земных года), прошедшего от исходной даты Великого Цикла в 3113 году н.э. Утренняя и вечерняя звезда, Венера тесно связана с Кетцалькоатлем-Кукульканом, поскольку Кетцалькоатль считался Владыкой Зари и Носителем Света - «Утренней Звездой» - и, одновременно, Проводником Мертвых и Хранителем Тайн Усопших - «Вечерней Звездой».

ПРИЛОЖЕНИЕ Д: 52 летний «Календарный круг»

Цолькин как 260 элементный Священный Календарь в сочетании с 365 дневным неполным земным годом - Хаабом - образует 52 летний цикл синхронизации. Это означает, что совпадение дня Священного Календаря и дня обычного календарного года происходит один раз в 18980 дней, или в 52 года. В то время, как 260 дневные циклы неизменно сменяют друг друга, 365 дневный Хааб состоит из 18 виналей по 20 дней в каждом и добавочным 5 дневным периодом ВАЙЕБ [Vayeb], фазой очищения и подготовки к наступлению следующего года. Таким образом, традиционная Майянская форма записи дат включает и дату 260 дневного цикла, и дату Хааба, например: 2 ИК 13 СОЦ, 13 AXAУ 1 ПОП.

Число 52 (13?4, 26?2), составляющее 1/5 260-элементного Гармонического Модуля, очевидно, является одним из ключевых чисел системы Майя; интересно, что оно входит в Большую печать Соединенных Штатов Америки (13 стрел, 13 звезд, 13 полос, 13 оливковых ветвей). 52 летний цикл представляет собой фрактал - примерно, одну сотую - 5200 тунового Великого Цикла. В поздних Майя, и в особенности у ацтеков, 52 летние циклы приобрели огромнейшее значение. Во времена испанского завоевания эти 52 летние циклы отсчитывались от дня Се Акатль (1 Тростник) года Се Акатль (1 Тростник), один из которых совпал с днем прибытия в Мексику Кортеса. Эта дата завершила тринадцать 52 летних циклов, так называемый «период Небес», и ознаменовала начало периода в девять 52 летних циклов - «период Ада», который закончится 16 августа 1987 года.

ИЕРОГЛИФИЧЕСКИЕ СИМВОЛЫ

ВОСЕМНАДЦАТИ ВИНАЛЕЙ И ПЕРИОДА ВАЙЕБ

Одна из сторон изящества 52 летнего цикла, согласовывающего 260 дневный Цолькин с 365 дневным Хаабом, заключается в том, что начальный день каждого из 52 неполных земных лет этого цикла может относиться лишь к одному из четырех Священных Знаков, причем смена этих Знаков подчиняется вращению направлений, или сторон света против часовой стрелки: МУЛУК (Восток); ИШ (Север); КАВАК (Запад) и KAH (Юг). В текущем цикле

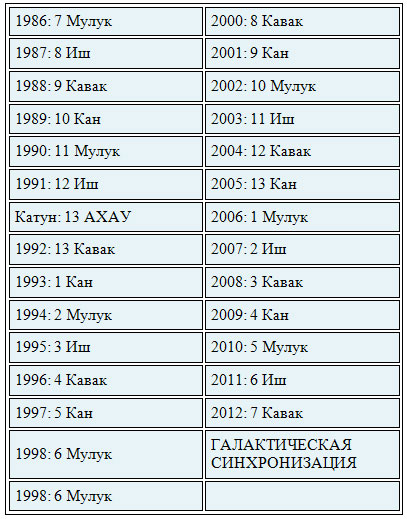
Одна из сторон изящества 52 летнего цикла, согласовывающего 260 дневный Цолькин с 365 дневным Хаабом, заключается в том, что начальный день каждого из 52 неполных земных лет этого цикла может относиться лишь к одному из четырех Священных Знаков, причем смена этих Знаков подчиняется вращению направлений, или сторон света против часовой стрелки: МУЛУК (Восток); ИШ (Север); КАВАК (Запад) и KAH (Юг). В текущем цикле майянский год начинается с одной и той же даты: 26 июля. 26 июля 1986 года является датой 7 МУЛУК; 26 июля 1987 года - 8 ИШ; 26 июля 1988 года - 9 КАВАК и так далее. В високосные годы период ВАЙЕБ состоит из шести, а не пяти дней, и за этим периодом следует дата 0 ПОП - это Новый Год Хааба, то есть в текущем цикле 26 июля всегда соответствует дате 0 ПОП (первый день Виналя имеет порядковый номер 0, а последний - 19)[10].

Символы 18 виналей и периода ВАЙЕБ приведены выше. Используя эти данные, информацию четвертой главы, а также описанную далее схему совпадения дней-планет, нетрудно построить еженедневный календарь и использовать его для практических занятий «астрологией» Майя.

СООТВЕТСТВИЕ 20 СВЯЩЕННЫХ ЗНАКОВ И ПЛАНЕТ

ЗЕМНЫЕ ГОДЫ С 1986 ПО 2012