Платоновы тела. Образец строгой красоты

Платоновы тела. Образец строгой красоты

Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.

Бертран Рассел

Вы можете сами того не подозревать, однако интерес к пространственной организации проявляется у вас с детства. Уже в двухлетнем возрасте человек сталкивается с правильными многогранниками, когда строит из детских кубиков дом или надежную крепость. Правильные многогранники встречаются в нашем окружении довольно часто. Некоторые сложно не заметить – пирамиды, детали соборов и храмов; другие невозможно рассмотреть невооруженным взглядом – вирусы, кристаллы.

Платоновы тела, или правильные многогранники – это многогранники, все стороны которых равны между собой и являются правильными многоугольниками. Сколько таких фигур может существовать? Казалось бы, правильный ответ должен исчисляться десятками и сотнями – ведь правильных многоугольников может быть очень много: треугольники, квадраты, пяти-, шести-, девяти, двеннадцатиугольники. Однако правильное число намного меньше – в природе существует всего пять Платоновых тел, а гранями правильных многогранников могут быть только три фигуры – треугольник, квадрат и пентагон (пятиугольник).

Правильные многогранники названы Платоновыми телами в честь древнегреческого философа, который уделял им много внимания в своей космологической теории.

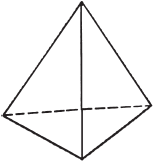
Платоновы тела, тетраэдр

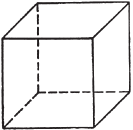
Платоновы тела, гексаэдр (куб)

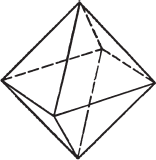
Платоновы тела, октаэдр

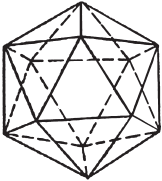
Платоновы тела, икосаэдр

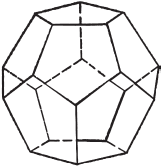
Платоновы тела, додэкаэдр

Среди Платоновых тел три образованы правильными треугольниками, одно – правильным квадратом, одно – правильным пятиугольником.

Первый многогранник – это тетраэдр. Его гранями являются правильные равносторонние треугольники. Три треугольника соприкасаются вершинами в одной точке, а основаниями образуют третий правильный треугольник – основание тетраэдра. Тетраэдр имеет меньше всего граней среди остальных многогранников и является аналогом плоского треугольника.

Следующее Платоново тело – октаэдр. Он также образован равносторонними треугольниками, но в этом случае тело имеет восемь граней. Октаэдр будто состоит из двух пирамид с четырехугольными основаниями, прижатыми друг к другу.

Если в одной точке соединить пять равносторонних треугольников и заполнить всю остальную выпуклую поверхность предполагаемой фигуры подобными сочетаниями, то получится икосаэдр – фигура с 20 гранями, представленными равносторонними треугольниками.

Следующий правильный многогранник – гексаэдр, или куб. Он образован шестью гранями – равносторонними квадратами.

Последнее Платоново тело – додекаэдр – состоит из 12 правильных пятиугольников. В каждой вершине соединяется по три пентагона.

Следующая многоугольная равносторонняя фигура – шестиугольник. Однако не существует такой возможности соединить больше, чем два шестиугольника в одной точке. А стало быть, и трехмерную плоскость они образовать не могут, равно как и многогранную правильную фигуру.

Данный текст является ознакомительным фрагментом.