Замороженная математика

Замороженная математика

Геоглифам Наска в определенной степени очень сильно «повезло», что ими в свое время заинтересовалась именно Мария Райхе. Дело в том, что Райхе была математиком по образованию.

Если бы изучением рисунков и линий на земле занимались лишь археологи и историки, то они, будучи сугубыми гуманитариями, несомненно, только воспроизводили бы общий вид геоглифов с той или иной степенью точности получаемого изображения и занимались бы в лучшем случае только анализом иконографии с позиций сравнения стилей. Так их обучают, и таким в итоге складывается не только их подход к описанию древних объектов, но и сам принцип восприятия ими объектов, их мышление.

Математик мыслит совсем по другому. Ему мало просто воспроизвести что-то в масштабе. Он пытается описать объект на своем, математическом языке. Именно поэтому Райхе не только составляла общую картосхему геоглифов Наска. Ее зарисовки и схемы изображенных в пустыне объектов сопровождаются многочисленными математическими параметрами отдельных элементов этих объектов, среди которых, например, радиус кривизны, расположение центра этой кривизны, углы между касательными в разных точках и тому подобное.

Рис. 73. Математические параметры фрагмента геоглифа Наска (схема М.Райхе)

Но стиль мышления математика таков, что исследователь не просто описывает изучаемый объект. Математик ищет возможные закономерности. И Райхе, в результате своих многолетних исследований, обнаружила, что закономерности в рисунках и линиях не просто есть – геоглифы Наска буквально «пронизаны» математикой!..

«Способ выполнения изобразительных фигур, и схема расположения линий и «центров» на поверхности плато подчинены математической логике. Так красота и гармония рисунков объясняется тем, что, как установила Мария Райхе, все кривые между собой и с прямыми линиями идеально сопряжены, то есть выполнены по строгим математическим законам. Математическим законам подчиняются и огибающие синусоидальных элементов, которые очень часто используются в изображениях» (А.Белоконь, «Фигуры пустыни Наска и круги на зерновых полях как результат энергетического воздействия НЛО на грунт», доклад на 10-й Юбилейной конференции «Уфология и биоэнергоинформатика», октябрь 2002 г.)

Подчиненность геоглифов жесткой математической логике произвела сильнейшее впечатление на астронома Джеральда Хокинса – руководителя экспедиции 1973 года, в ходе которой были измерены геодезические параметры многих линий и была опровергнута гипотеза древней обсерватории. Описывая эту экспедицию в жаркую пустыню Наска, Хокинс использовал очень эмоциональное, но емкое выражение – «жизнь в аду замороженной математики».

Однако для нас, пожалуй, более важным является не эмоциональное состояние Хокинса, а тот факт, который был им выявлен в ходе его экспедиции. Согласно проведенным в этой экспедиции измерениям, большие линии плато Наска сделаны на пределе современных (!) приемов геодезии и аэрофотосъемки. Их среднее отклонение по направлению не превышает 9 угловых минут. То есть всего два с половиной метра на целый километр длины! И это при том, что очень многие из линий пересекают овраги и небольшие холмы. Для примитивных культур наска и паракас это – невозможный результат. Тут требуются именно весьма развитые измерительные технологии!..

Рис. 74. Линии сделаны на пределе современных геодезических возможностей

Целый ряд исследователей обратили внимание на одно странное обстоятельство. Те изображения на плато Наска, которым, по всей логике, полагалось бы быть симметричными (паук, кондор и другие), на самом деле обладают весьма ярко выраженной асимметрией. Эта странность настолько бросалась в глаза, что заставляла искать какое-то логическое объяснение. И в последние годы появился целый ряд публикаций, в которых авторы независимо друг от друга приходят к одному и тому же выводу – нарушения симметрии в геоглифах Наска является вовсе не результатом небрежности их создателей, а неизбежным следствием того, что древние авторы… рисовали проекции трехмерных изображений!

Вот, что пишет, например, по этому поводу И.Алексеев:

«Кондор нарисован в двух пересекающихся под небольшим углом плоскостях (см. Рис. 29-ц). Пеликан, похоже, в двух перпендикулярных. Очень интересный 3-d вид имеет наш паучок (1 – оригинальное изображение, 2 – выпрямленное, с учетом плоскостей на рисунке). И это заметно на некоторых других рисунках… А посмотрите, как остроумно заложен трехмерный объем в дереве (см. Рис. 75). Это как бы сделано из листа бумаги или фольги, я просто распрямил одну ветку» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

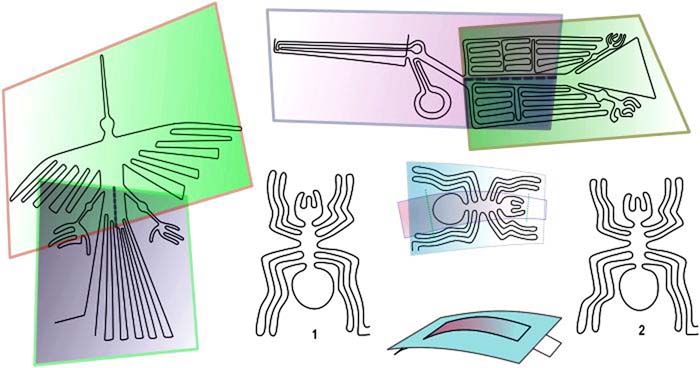
Рис. 29-ц

Киевский геолог, специалист по историческим артефактам Р.С.Фурдуй и его коллеги продвинулись еще дальше. Они провели компьютерный эксперимент с изображением кондора, который показал, что соответствующее искажение формы рисунка могло произойти в том случае, если трехмерный оригинал проецировался на поверхность пустыни под углом 14° к горизонту с высоты 355 метров над землей!..

Только представьте себе древних индейцев-шаманов, которые умудряются полторы тысячи лет назад не только создать воздушный шар и подняться на нем на высоту трех с половиной сотен метров, но и, держа в руках трехмерную фигурку кондора, руководить с этой высоты действиями индейцев-рабочих на земле так, чтобы в итоге получить точную проекцию фигурки. Вряд ли кто-то будет возражать тому, что картинка получается уж совсем за гранью реальности…

Рис. 75. Передача трехмерности в геоглифе «дерево» (по И.Алексееву)

И.Алексеев решил попробовать сделать исходную трехмерную фигуру странного существа, которая при проецировании на землю давала бы известный геоглиф, похожий на цыпленка с девятью пальцами, и получил любопытный результат (см. Рис. 30-ц).

Рис. 30-ц

«С лапами пришлось помудрить, древние их изображали слегка утрированно, да и никакое существо не ходит на цыпочках. А в целом получилось сразу, ничего даже додумывать не пришлось – все есть в рисунке (специфический сустав, выгнутость тела, положение «ушей»). Что интересно – фигура изначально получилась сбалансированной (стояла на ногах). Автоматически возник вопрос, а что это, собственно, за зверюшка? И вообще, откуда древние черпали сюжеты для своих замечательных экзерсисов на плато?» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

В 2010 году Алексееву удалось-таки решить задачу, которую так до конца и не смогла решить Мария Райхе. Он нашел те самые математические закономерности, которые заложены в геоглифах Наска. Причем вышел он на это решение буквально полуинтуитивным образом.

Пытаясь воспроизвести рисунки Наска с помощью компьютера в простеньком графическом редакторе Paint.net, он обнаружил, что чем меньше линий, наносимых  от руки, и чем больше используется встроенных в редактор способов создания линий с изменяемой кривизной – тем больше сходства с реальными геоглифами. Как он сам пишет, у него даже порой возникало ощущение, что авторы рисунков на плато Наска использовали при их создании то же самое программное обеспечение!..

Но для создания линий с изменяемой кривизной в современных графических редакторах широко используются так называемые кривые Безье.

Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году. Метод кривых Безье был разработан в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где этот метод применялся для проектирования кузовов автомобилей. Благодаря простоте задания и управления изменениями, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий.

Рис. 76. Сергей Натанович Бернштейн

«И вот, в один прекрасный момент я вдруг обнаружил, что при определенной сноровке в работе с кривыми Безье программа иногда сама достаточно похоже прорисовывала контуры. Сначала это было заметно на скруглениях ног паука, когда без моего участия эти скругления становились почти идентичными оригинальным. Далее, при правильных позициях узлов и при их объединении в кривую, линия иногда почти точно повторяла контур рисунка. И чем меньше узлов, но более оптимальна их позиция и настройки – тем больше сходства с оригиналом.

Вообще, паучок – практически одна кривая Безье (правильнее сплайн Безье, последовательное соединение кривых Безье), без окружностей и прямых. При дальнейшей работе возникло ощущение, перераставшее в уверенность, что этот неповторимый «насканский» дизайн – и есть сочетания кривых Безье и прямых. Правильных кругов или дуг почти не наблюдалось.

А не кривые ли Безье пыталась описать Мария Райхе, математик по образованию, делая многочисленные замеры радиусов?» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

Рис. 77. Прорисовка геоглифа «паук» с помощью кривых Безье (по И.Алексееву)

«Но по-настоящему мастерством древних я проникся при прорисовке больших рисунков, где встречались почти идеальные кривые огромных размеров. Еще раз напомню, что целью прорисовок была попытка посмотреть на эскиз, на то, что было у древних перед нанесением на плато. Я старался свести к минимуму собственное творчество, прибегая к дорисовке поврежденных мест лишь там, где логика древних была очевидна (как, например, хвост у кондора, выпадающее и явно современное скругление на теле паука)» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

Алексееву удалось таким образом воспроизвести практически все основные рисунки, известные на плато Наска. В дальнейшем, опираясь на материалы его статьи, на сайте форума Лаборатории Альтернативной Истории был проведен своеобразный «динамический» эксперимент. Человек пытался прорисовать от руки изображение паука поверх фотографии в специализированной графической программе. Рука, естественно, при этом дрожала и сбивалась. Программа же сглаживала «ручные» огрехи в соответствии с алгоритмом кривых Безье. При этом итоговая кривая автоматически почти идеально ложилась на оригинальную фотографию!..

Райхе лишь чуть-чуть не дошла до этого решения сформулированной ей же задачи выявления математических закономерностей геоглифов плато Наска, хотя основы этих закономерностей и были прописаны Бернштейном на заре ее молодости. Не дошла, скорее всего, только потому, что она не застала того времени, когда компьютерное использование кривых Безье стало широко доступным.

Ясно, что какие-либо рассуждения о знании индейцами культур наска и паракас кривых Безье находятся далеко за гранью сколь-нибудь разумной логики. Современных компьютеров с графическими программами у них тоже не было. Соблюсти же соответствующие математические закономерности могла только такая цивилизация, которая имела уровень развития, как минимум сопоставимый с нашим.

Выходит, что Дэникен был прав – геоглифы не только обращены к небесным зрителям, но и созданы ими. И индейцы местных культур наска и паракас явно не имеют никакого отношения к этим небесным зрителям.

Только теперь это уже не просто предположение, а гипотеза, имеющая строгое математическое обоснование!

Вполне возможно, что если не сами индейцы, то их предки знали о том, что геоглифы Наска создавались высоко развитой цивилизацией. И создавались вовсе не вручную, а с помощью специальных механизмов.

«…в этой связи интерес представляет следующая картинка (см. Рис. 31-ц). Достойный конкурент известному «астронавту» из храма надписей в мексиканском Паленке. Возможно, что это эпизод из какого-нибудь недошедшего до нас насканского мифа, но то, что «котобог», пожирающий предметы, похожие на камни, используется как некое транспортное средство для воина с копьеметалкой и полным боекомплектом – изображено достаточно недвусмысленно» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

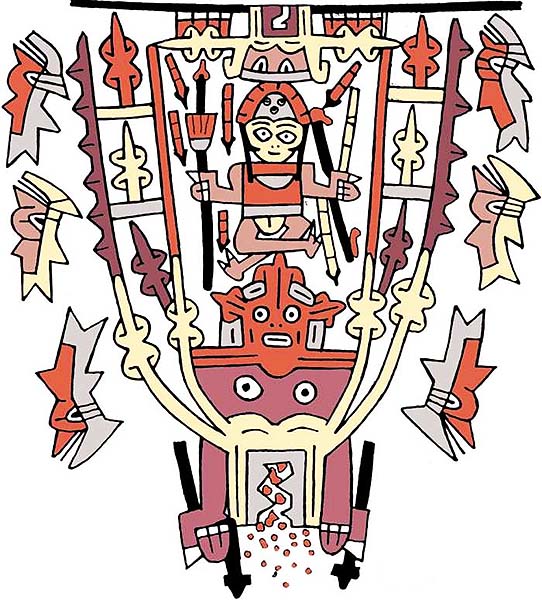
Рис. 31-ц

И еще один момент, подмеченный Алексеевым. Занимаясь экспериментированием с кривыми Безье при прорисовке так называемого «пеликана» – огромного геоглифа, занимающего площадь 280 на 400 метров, он обнаружил довольно странную деталь.

Рис. 78. «Пеликан»

«Единственный рисунок, который из-за своих размеров и идеальных линий выглядит на прорисовке абсолютно так же, как и в пустыне (и на эскизах древних соответственно). Называть это изображение пеликаном не совсем корректно. Длинный клюв и нечто, похожее на зоб еще не означает пеликана. Древние не обозначили главную деталь, что делает птицу птицей – крылья. И вообще это изображение нефункционально со всех сторон. Ходить по нему нельзя – оно не замкнуто. Да и как на глаз попадать – опять прыгать? С воздуха рассматривать в силу специфичности деталей неудобно. С линиями оно тоже особо не сопрягается. Но, тем не менее, сомнений нет, этот объект создавался намеренно – гармонично смотрится, идеальная кривая уравновешивает трезубец (судя по всему, поперечный), клюв сбалансирован расходящимися прямыми позади. Я не мог понять, почему от этого рисунка остается ощущение чего-то очень необычного. А все очень просто. Мелкие и тонкие детали разнесены на значительное расстояние, и чтобы понять, что перед нами – мы должны переводить взгляд с одной мелкой детали на другую. Если же отодвинуться на значительное расстояние, что бы охватить рисунок целиком, то вся эта мелкота как бы сливается и смысл изображения теряется. Такое ощущение, что этот рисунок создавался для восприятия существом с другим размером «желтого» пятна – зоны наибольшей остроты зрения в сетчатке глаза. Так что если какой рисунок и претендует на неземную графику – то наш пеликан первый кандидат» (И.Алексеев, «Геоглифы Наска. Некоторые наблюдения»).

Данный текст является ознакомительным фрагментом.