Абидосская таблица

Абидосская таблица

Дадим слово самому Морозову:

«… что скажете вы по поводу следующего анекдота об Якове Бернулли, отце современной математической теории вероятностей.. ?

Когда Яков Бернулли был еще юношей и сидел, занимаясь в своей комнате в Базеле, пошел сильный град, который выбил стекло его окна, и на полу его комнаты оказалось 77 градин, расположившихся своеобразными группами. Он классифицировал их по их расстояниям от наружной стены и насчитал 15 групп, которые и отметил на полу меловыми линиями, параллельными стене. Стекло было вставлено в окно, но на следующий день пошел новый град, снова пробил стекло в окне и даже в другом месте, и, когда град кончился, он снова сосчитал попавшие к нему градины, и, к удивлению его, оказалось, что и теперь их лежит на полу тоже 77 градин и, можете себе вообразить? — они расположились между его меловыми линиями совершенно так же, как и прежние, только на месте предпоследней градины оказалось мокрое место, как будто бы она упала уже растаяв.

А в деталях вышло следующее.

Между его 1–й и 2–й линиями оказалось, при обоих случаях, как раз 8 градин, очень старого, особого вида, и первыми из них легли две крупные градины.

Между 2–й и 3–й линиями оказалось как раз 5 градин и в том и в другом случае, и вторая из них была тоже более крупной.

Между 3–й и 4–й линиями оказалось 7 градин и в том и в другом случае, и вторые две легли в каждом особо от других.

Между 5–й и 6–й линиями в первом случае оказались 4 такие огромные и своеобразные градины, каких он ни разу не видал в своей жизни, да и во втором случае оказались и такие огромные и своеобразные градины, каких он ни разу не видал в своей жизни…

И между всеми остальными его линиями получилось такое же точное числовое и даже качественное совпадение в обоих случаях, а последние градины у них были похожи на драгоценные камни, хотя оба града были независимы друг от друга, и пробоины в стеклах были различны. Это удивительное совпадение так заинтересовало молодого Якова Бернулли, что он принялся за изучение закона случайных совпадений и открыл свою знаменитую формулу в математической теории вероятностей…

— Позвольте! — прерываете вы, конечно, меня. — В тот момент, когда он открыл бы свою знаменитую формулу, он убедился бы, что оба эти града, или, по крайней мере, второй из них видел только во сне, так как сама же теория вероятностей показывает, что такого совпадения и по общему числу 77 и по отдельным группам в реальности не может быть. Даже если бы дело шло об одном и том же граде, падавшем в комнату через два одинаковых отверстия, то вероятность адекватного совпадения уменьшалась бы более, чем обратно пропорционально возрастанию числа упавших градин.

А здесь и обе пробоины независимы по своей величине и оба града независимы по своей продолжительности!… Это требует возведения 77 более чем в третью степень. А разделение градин на 15 одинаковых по качеству и количеству групп, причем в обоих случаях четвертая группа является исключительными градинами, которым равных не приходилось видеть в жизни, может быть только в волшебной сказке…

И вот эту–то самую волшебную сказку мы и видим в приложенной таблице (см. рис. 1 — Авт.), где я дал сопоставление знаменитой в египтологии родословной Рамзеса Великого (имя которого Ра–Мессу значит «бог родил его») и знаменитой в «священной истории» родословной богорожденного же Иисуса Христа.

Скажите сами: не похоже ли это на сон? Для математика — это явное сновидение. Рассмотрим же эту ночную грезу в деталях» ([1], стр. 380—382).

Далее Морозов приводит список фараонов Абидосской таблицы (это и есть «родословная Рамзеса») в сопоставлении с родословной Иисуса по Евангелиям от Матфея и Луки. Мы опустим это, поскольку имена в обоих списках, как мы уже знаем, вполне «условны», а при замене их цифрами мы возвращаемся к рис. 1. Мы ограничимся тем, что приведем комментарии Морозова.

«I. Первые 8 царей Абидосской таблицы от Мены до Кебху выделены греческими авторами Евсевием, Африканом и другими в 1–ю (Тинитскую) династию и соответственно им первые 8 библейских патриархов (на левой стороне таблицы) представляют из себя особую группу, называемую допотопными патриархами, так сказать тоже «династия»…

Сравнение чисел предков Рэ–Мессу Миамуна в последовательных псевдодинастиях египетских царей по Абидосской таблице с числами предков Иисуса–Миссии в их естественных группах по Евангилею Луки (гл. 3).

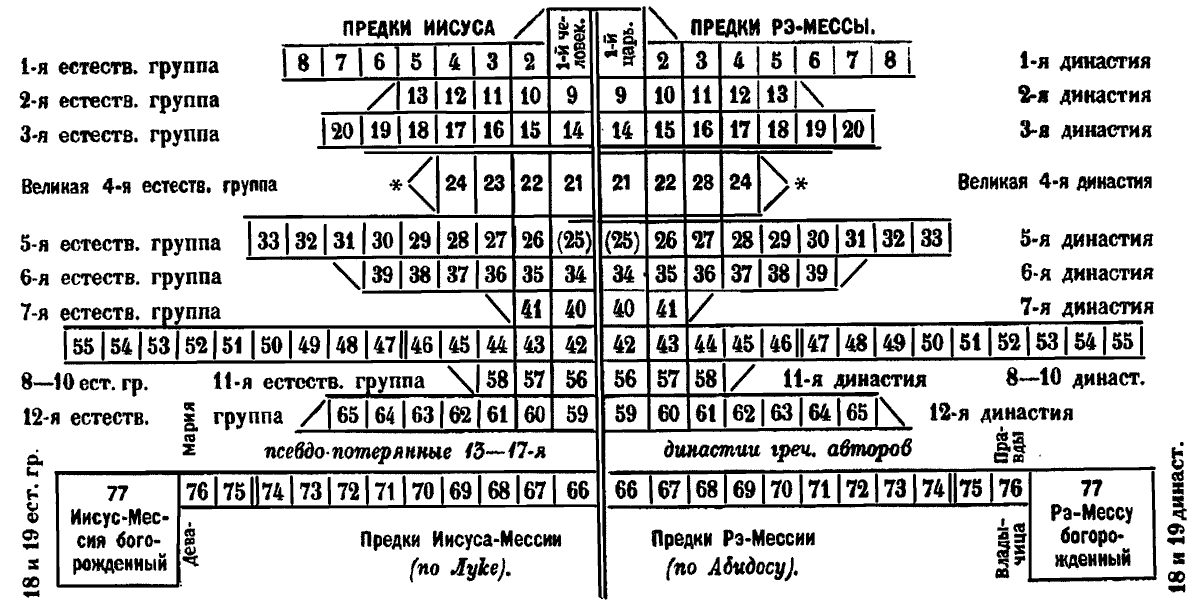
 Параллелизм обеих сторон полный: каждый из 76 египетских предков Рэ–Мессы имеет своего изотопа в предках Иисуса–Мессии у Луки. Такое совпадение и общего числа, и отдельных групп возможно по теории вероятностей лишь в двух случаях:

1) если Рэ–Мессу тождественен с Иисусом–Мессией или

2) если это были два одновременные и различно знаменитые двоюродные брата.

 Если же допустим, что все это миф, то — это тот же самый миф в двух разно–национальных ответвлениях.

 Второй вывод: или библейские патриархи представляют из себя египетских царей под другими прозвищами, или наоборот. Другого выхода нет.

В ней первый египетский царь Мена соответствует первому библейскому патриарху Адаму. Если еврейское начертание имени Адам (АДМ) сравнить с иероглифическим начертанием Мены (МНА) и прочесть этот иероглиф (как допускается в египтологии) снизу вверх, то получим АДМ—АНМ, причем звук Н представляет, в сущности, звук Д с резонансом носовой полости.

II. Следующие 5 египетских царей… выделены теми же греческими авторами во 2–ю (Тинитскую же) династию, а в Библии их изотопы выделяются в естественную группу 5–ти послепотопных патриархов с присоединением к ним Ноева отца (Ламеха), и в иероглифе Ноя (точнее его аналога, фараона. — Авт.) показаны 3 сына.

III. Следующие 7 египетских царей выделяются египтологами в 3–ю (Мемфисскую) династию, а в Библии их изотопы выделяются в естественную группу потомков Евера…

IV. Следующие 4 египетские царя так своеобразно знамениты, как никакие другие в египетской истории, по великим пирамидам, воздвигнутым над ними. Первый из них Хуфу (или Хеопс греческих авторов)…; второй Дедеф–Ре, пирамиду для которого греческие авторы не указывают…; третий Хеф–Ре, над которым высится вторая великая пирамида, и четвертый Менкав–Ре (или Микерин греческих авторов), над прахом которого воздвигнута третья великая пирамида.

Это такая своеобразная «династия», подобной которой мы не находим в человеческой истории. А кто же является их изотопами по Евангелию Луки (да и по Библии)? Взгляните на левую сторону таблицы и вы поразитесь. Это Авраам, отец множества народов (или по буквальному переводу АБ–РМ — отец Римской империи). Это Исаак, его сын, соответствующий Дедеф–Ре, а затем Иаков–Израиль, родоначальник царства Израильского, успешно боровшийся с самим богом Громовержцем, а четвертый, соответствующий Менкав–Ре, — это Иуда Иаковлев, родоначальник царства Иудейского… Опять имена, равных которым нет в древней истории.

… V. Пятая династия египетских царей, в отличие от только что разобранной и называемой Мемфисской, носит у греческих авторов имя Елефантинской династии. Как в Абидосской таблице, так и в Евангелии от Луки она состоит из 8 царей, в главе которых поставлен в Евангелии Ес–Ром, а его египетским изотопом является Ус–Каф, в память которого, как и его 7 потомков, воздвигнуты пирамиды меньшей величины. Это все непосредственные предки «святого царя Давида».

VI. Следующие 6 царей Абидосской таблицы, начиная от Тота и кончая Мерен–Ре Цефамцафом, составляют по греческим авторам VI династию, а в евангельской родословной Иисуса ей соответствуют 6 потомков царя Давида (замыкающиеся Соломоном — Авт.). Давид по–библейски пишется ДУД или ДОД и должен бы был произноситься Дода, что очень созвучно с его египетским изотопом Тота (ТТА), так как Д отличается от Т только прибавкой резонанса горла. Интересно отметить, что в родословной Матвея здесь отсутствуют четыре промежуточных царя, вставленные как в Евангелии от Луки, так и в Абидосской таблице между Давидом–Тотом и Соломоном Премудрым — Мерен–Ре Цефамцафом, переименованным у Луки в Елиакима. Не показывает ли это, что Матвей пользовался более древней родословной, чем Лука, списавший целиком всю Абидосскую таблицу?» ([1], стр. 388—393).

В следующих династиях VII—XI греческие авторы не дают списка царей, а лишь упоминают, что были и такие династии. Абидосская таблица дает для этого периода 19 имен. Сопоставляя их с именами из евангельского родословия Иисуса, Морозов оказывается в состоянии довольно уверенно распределить эти 19 имен по династиям. Мы этим заниматься не будем.

Затем Морозов переходит к следующей, XII династии. Это династия завоевателей, гиксосов, якобы одного из пастушеских народов. Как мы увидим ниже, при более подробном обсуждении египетских династий, эта характеристика гиксосов, да и сам факт завоевания ими Египта оказывается плодом измышлений историков, пытавшихся дать рациональное объяснение информации греческих авторов, что эта династия состояла из царей–пастухов.

У Луки этим «пастухам» соответствуют правители Иудеи Маккавеи (имя которых по Морозову означает «молотильщики»). Их ровно столько же (семь), сколько и царей в Абидосском списке.

«В родословной Матвея вся эта династия отсутствует. Значит, он взял свою родословную Иисуса из более старинного документа, чем Абидосская таблица (утверждение, что более короткие родословные являются более древними, было нами обсуждено в гл. 8, § 5 — Авт.), в которую, как и в Евангелие Луки, эта династия была вдвинута исключительно для того, чтобы удлинить историю египтян и «иудеев», представлявших, очевидно, два народа под одной династией» ([1], стр. 394).

Кончается Абидосская таблица вполне замечательным образом. Непосредственным предшественником Ра–Мессу показана женщина по имени «Владычица правды»! Она вполне соответствует деве Марии, отсутствующей у Луки. Морозов заключает:«Это отсутствие девы Марии в родословии Иисуса и есть то «мокрое пятно от предпоследней растаявшей градины», о которой я говорил в моей аллегории. Два града, проскочившие в комнату Якова Бернулли, каждый в количестве 77 градин, это были у меня две только что разобранные здесь родословные. Оба града были представлены у меня выпавшими в два разные дня для того, чтобы символизировать две культуры, «иудейскую» и «египетскую», считаемые до сих пор различными, а то, что для каждого града я, кроме того, сделал еще разные пробоины в стеклах комнаты творца теории вероятностей, символизирует априорное предположение, что обе приведенные здесь родословные написаны независимо друг от друга.

И вот окончательный результат: если вы, несмотря на мое сравнение обеих родословных и в общем, и по частям, все–таки будете утверждать, что они представляют «счастливое случайное совпадение» и будете вводить это утверждение в учебники истории, то вы вместе с тем должны будете признать, что и рассказанный мною анекдот об Якове Бернулли не представляет тоже ничего невероятного, и его можно будет тоже ввести в учебники математики…» ([1], стр. 397—398).